Are you searching for – Mastering Two’s Complement: A Compressive Guide
Then you are at Right Place.
The Complete and Official Information of Mastering Two’s Complement: A Compressive Guide
Mastering Two’s Complement: A Compressive Guide

In a number system, a two’s complement is a well-known technique for representing signed integers in binary form. It gives the best way to perform arithmetic operations on binary numbers in digital systems and computer architecture.
The decimals and binary numbers could be converted into two’s complements with the help of various techniques. In this post, we will learn the basics of the two’s complement with the help of solved examples.
What is Two’s Complement?
In mathematics, a 2’s complement is an operation that is essential for representing signed numbers in 0 and 1 form. It is used to represent the negative numbers in digital language as the one’s complement is applicable for the positive integers only.
The indication of the positive and negative numbers could be determined with the least significant bit as:
- If the least significant bit is 1 it represents a negative number.
- If the least significant bit is 0 it represents a positive number
The manipulation of positive and negative numbers in the form of 0 and 1 in digital language and operations can be done easily with the help of 2s complement.
How to convert binary numbers into 2s complement?
The two’s complement representation of a binary number can be done by following the below steps.
- Take the binary number.
- Complete the bit system.
- Invert all the digits of binary numbers i.e., 0s to 1s and 1s to 0s. This process of inverting numbers is said to be the transpose of a binary number.
- Add 1 to the most significant bit of LSB
- The resulting number would be the two’s complement of a binary number.
Examples
Example 1:
Convert 10101011101011 into the two’s complement. If the system is 16-bit.
Solution
Step 1: Take the binary number and complete the 16-bit system of the given number.
given number = 10101011101011
12-bit will be obtained by adding 0s to the right of the given number.
16-bit number = 0010101011101011
Step 2: Now take the transpose of the above 12-bit binary number by inverting all 0s to 1s and 1s to 0s.
12-bit number = 0010101011101011
Inverted Number = 1101010100010100
Step 3: Now add 1 to the most significant bit of the above inverted binary number.
1 1 0 1 0 1 0 1 0 0 0 1 0 1 0 0
+ 1
1 1 0 1 0 1 0 1 0 0 0 1 0 1 0 1
Hence, the given 16-bit binary number is converted to a signed binary number.
Example 2
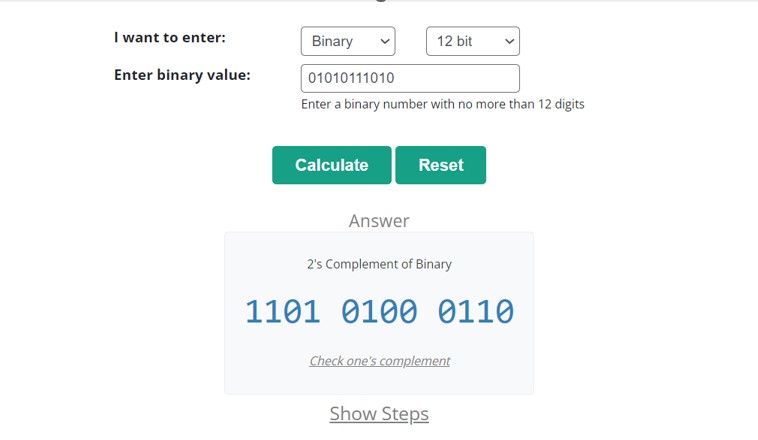
Convert 01010111010 into the two’s complement. If the system is 12-bit.
Solution
Step 1: Take the binary number and complete the 12-bit system of the given number.
given number = 01010111010
12-bit will be obtained by adding a 0 to the right of the given number.
12-bit number = 001010111010
Step 2: Now take the transpose of the above 12-bit binary number by inverting all 0s to 1s and 1s to 0s.
12-bit number = 001010111010
Inverted Number = 110101000101
Step 3: Now add 1 to the most significant bit of the above inverted binary number.
1 1 0 1 0 1 0 0 0 1 0 1
+ 1
1 1 0 1 0 1 0 0 0 1 1 0
Hence, the given 12-bit binary number is converted to a signed binary number.
A two’s complement calculator is an alternative way to find the 2s complement of the given binary numbers. Below is a picture of the above example solved by this tool.
How to convert decimal numbers into 2s complement?
The two’s complement representation of a decimal number can be done by following the below steps.
- Take the given decimal number
- Convert the given decimal number into a binary number.
- Complete the bit system.
- Invert all the digits of binary numbers i.e., 0s to 1s and 1s to 0s. This process of inverting numbers is said to be the transpose of a binary number.
- Add 1 to the most significant bit of LSB
- The resulting number would be the two’s complement of a binary number.
Examples
Example I:
Convert 192 into the two’s complement.
Solution
Step 1: First of all, take the given decimal number.
positive decimal number = 192
Step 2: Now convert the given decimal number into a binary number.
| 2 | 192 |
| 2 | 96 – 0 |
| 2 | 48 – 0 |
| 2 | 26 – 0 |
| 2 | 12 – 0 |
| 2 | 6 – 0 |
| 2 | 3 – 1 |
| 1 – 1 |
The binary number of 192 is 11100000
Step 3: Take the binary number and complete the 12-bit system of the given number.
Binary number = 11100000
12-bit will be obtained by adding 0s to the right of the given number.
12-bit number = 000011100000
Step 4: Now take the transpose of the above 12-bit binary number by inverting all 0s to 1s and 1s to 0s.
12-bit number = 000011100000
Inverted Number = 111100011111
Step 5: Now add 1 to the most significant bit of the above inverted binary number.
1 1 1 1 0 0 0 1 1 1 1 1
+ 1
1 1 1 1 0 0 1 0 0 0 0 0
Hence, the given 12-bit binary number is converted to a signed binary number.
Example II
Convert 1194 into the two’s complement.
Solution
Step 1: First of all, take the given decimal number.
positive decimal number = 1194
Step 2: Now convert the given decimal number into a binary number.
| 2 | 1194 |
| 2 | 597 – 0 |
| 2 | 298 – 1 |
| 2 | 149 – 0 |
| 2 | 74 – 1 |
| 2 | 37 – 0 |
| 2 | 18 – 1 |
| 2 | 9 – 0 |
| 2 | 4 – 1 |
| 2 | 2 – 0 |
| 1 – 0 |
The binary number of 1194 is 10010101010
Step 3: Take the binary number and complete the 12-bit system of the given number.
Binary number = 10010101010
12-bit will be obtained by adding 0s to the right of the given number.
12-bit number = 010010101010
Step 4: Now take the transpose of the above 12-bit binary number by inverting all 0s to 1s and 1s to 0s.
12-bit number = 010010101010
Inverted Number = 101101010101
Step 5: Now add 1 to the most significant bit of the above inverted binary number.
1 0 1 1 0 1 0 1 0 1 0 1
+ 1
1 0 1 1 0 1 0 1 0 1 1 0
Hence, the given 12-bit binary number is converted to a signed binary number.
How to Perform Arithmetic Operations on Two’s Complement?
The 2s complement allows one to add or subtract two signed binary numbers. The addition and subtraction of two signed binary numbers is the same as in regular binary addition and subtraction. The carry system of the two’s complement also includes if necessary.
For Addition
For the addition of two’s complement numbers, follow the below steps.
- Take two signed binary numbers
- Make sure the bit of both numbers would be the same.
- Start adding bits from the right-most bit to left most bit.
- The sum of two 1s would be 0 and the 1 should be carried to the next bit.
For Example
Add 101010100 and 11100011
Solution
Step 1: Take the given two’s complement numbers.
Number 1 = 101010100
Number 2 = 11100011
Step 2: Make the same number of bits.
Number 2 has 8 bits, add 0 to the rightmost side
Number 2 = 011100011
Step 3: Now add them.
1 0 1 0 1 0 1 0 0
+ 0 1 1 1 0 0 0 1 1
1 0 0 0 1 1 0 1 1 1
For Subtraction
For the subtraction of two’s complement numbers, follow the below steps.
- Take two signed binary numbers
- Make sure the first number would be a greater bit or the same as the second one.
- Start subtracting bits from the right-most bit to left most bit.
- The difference of two 1s would be 0 and the 2 should be carried from the previous if 0 could be subtracted from the 1.
For Example
Subtract 101110111 and 10111011
Solution
Step 1: Take the given two’s complement numbers.
Number 1 = 101110111
Number 2 = 10111011
Step 2: Now add them.
1 0 1 1 1 0 1 1 1
– 1 0 1 0 1 0 1 1
0 1 1 0 0 1 1 0 0
Conclusion
The basics of the two’s complement will allow you to master it. We have explained the conversions and arithmetic operations of signed binary numbers. Now you can grab and understand the concept of twos complement by seeking guidance from this post.
Thanks to All Beloved Readers.

